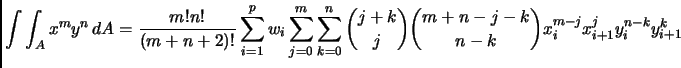- Preface,
page vii,
the editor-in-chief's email address is listed as
zwilling@world.std.com. This is now outdated, the correct
email address is zwillinger@alum.mit.edu.
This entry updated before 7 March 2001.
- Preface,
page vii,
the following text should be added:
Errata for this book will be maintained at
http://errata.mathtable.com
This entry updated before 7 March 2001.
- Section 1.1.2,
REPRESENTATION OF NUMBERS,
page 4,
line 18 presently has
``
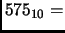 3BA
3BA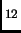 '', which is incorrect.
It should have been
``
'', which is incorrect.
It should have been
``
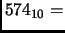 3BA
3BA ''.
''.
(Thanks to Richard Hughes for this correction.)
This entry last updated 25 Februrary 2002.
- Section 1.1.4,
ROMAN NUMERALS
page 5:
(Thanks to Glebb Leider for these corrections.)
This entry updated before 7 March 2001.
- Section 1.2.6,
FACTORIALS,
page 15,
lines 7-8, we presently have
...(also called the falling factorial ...
(sometimes
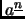 ) ...
) ...
This is incorrect. It should have been
...(also called the rising factorial ...
(sometimes
 ) ...
) ...
[This brings the description into line with, e.g.,
D. Knuth, Art of Computer Programming, Vol I,
3rd Edition, Section 1.2.5, Permutations and
Factorials, page 50.]
(Thanks to David Gehrig for this correction.)
This entry updated before 7 March 2001.
- Section 1.2.6,
FACTORIALS,
page 15,
the following text should be added
(Thanks to David Cantrell for these corrections.)
This entry updated before 7 March 2001.
- Section 1.3.2,
GENERAL PROPERTIES,
page 31,
item number 9,
Holder's inequality is listed as

This is incorrect. It should have been
(note the exponents on the terms)
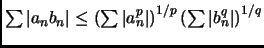
(Thanks to Alain Boulanger for this correction.)
This entry updated before 7 March 2001.
- Section 1.3.4,
TYPES OF SERIES,
page 35,
Taylor series,
item number 2, Lagranges's form:
we presently have
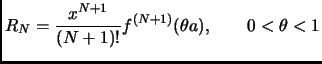
This is incorrect. It should have been

(Thanks to Richard E. Stone for this correction.)
This entry updated before 7 March 2001.
- Section 1.3.4,
TYPES OF SERIES,
page 36,
Other types of series,
item number 2,
Arithmetic power series: the left hand side of the equation is shown as
as
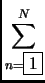
This is incorrect.
It should have been (note the summation should start at 0, not 1)
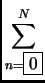
(Thanks to Greg Iles for this correction.)
This entry updated before 7 March 2001.
- Section 1.3.10,
INFINITE SERIES,
page 40,
the following should be added:
(Thanks to Barry Pasternack for this addition.)
This entry updated before 7 March 2001.
- Section 1.4.4,
EXPANSIONS OF BASIC PERIODIC FUNCTIONS
page 50,
This entry updated before 7 March 2001.
- Section 1.5.15,
TABLE OF TRANSFORMATIONS,
page 57,
presently has the following table entry (line 9)

This is incorrect and should be:

(Thanks to Kosa Gabor for this addition.)
This entry updated before 7 March 2001.
- Section 1.6.5,
METRIC SPACE,
page 66,
presently has the following line
positive definiteness:
 for all
for all 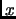 ,
, 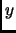 in
in
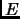 , and
, and
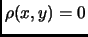 if and only if
if and only if 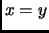 .
.
This is incorrect and should be (note that ``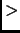 '' is replaced with
``
'' is replaced with
``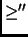 ):
):
positive definiteness:
 for all
for all 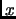 ,
, 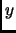 in
in
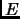 , and
, and
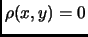 if and only if
if and only if 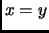 .
.
(Thanks to Paul Stanford for this correction.)
This entry updated before 7 March 2001.
- Section 1.7,
GENERALIZED FUNCTIONS,
page 72,
item number 7 was
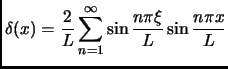 for
for 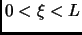 (Fourier sine series)
(Fourier sine series)
which is incorrect. It should have been
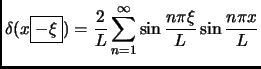 for
for  (Fourier sine series)
(Fourier sine series)
This entry last updated 5 October 2001.
- Section 1.7,
GENERALIZED FUNCTIONS,
page 72,
the Heaviside function is defined as
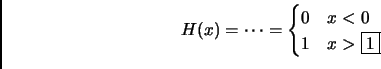 .
.
This is incorrect. It should have been
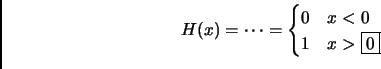 .
.
(Thanks to Catherine Roberts for this correction.)
This entry updated before 7 March 2001.
- Section 2.1.4,
PARTIAL FRACTIONS,
page 81,
- Repeated linear factor:
The center of the page now has, in part
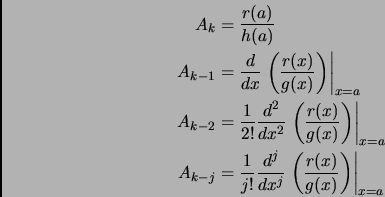 |
(1) |
This is incorrect. It should have been (note that the 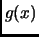 's should
have been
's should
have been 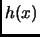 's)
's)
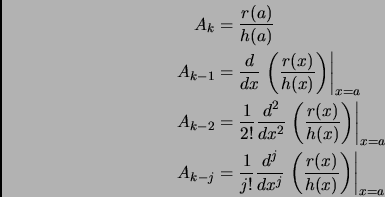 |
(2) |
- Single quadratic factor:
When
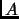 and
and 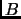 are both real, if after multiplying the equation by
are both real, if after multiplying the equation by
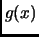 a root of
a root of 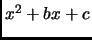 is substituted for
is substituted for 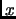 , then the values
of
, then the values
of 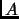 and
and 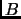 can be inferred from this single complex equation by
equating real and imaginary parts.
can be inferred from this single complex equation by
equating real and imaginary parts.
Similarly for Repeated quadratic factors. In other words,
the number of equations needed is half the number stated.
(Thanks to David M. Bradley for these corrections.)
This entry updated before 7 March 2001.
- Section 2.2.2,
CUBIC POLYNOMIALS,
page 82,
the second paragraph is now
The solutions are given by
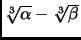 ,
,
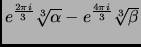 , and
, and
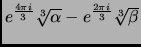 , where
, where
This is incorrect. It should have been (note the signs)
The solutions are given by
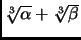 ,
,
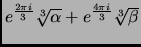 ,
and
,
and
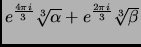 , where
, where
This entry updated before 7 March 2001.
- Section 2.3.1,
Values,
page 87,
presently has ``There are 32 Carmichael numbers less than one million''
which is incorrect, it should have been
``There are 32 Carmichael numbers less than one
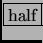 million''.
million''.
This entry last updated 25 Februrary 2002.
- Section 2.3.9,
PRIME NUMBERS,
page 94,
line
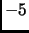 , we presently
have
, we presently
have

This is incorrect. It should have been

(Thanks to See Chew for this correction.)
This entry updated before 7 March 2001.
- Section 2.5.4,
DETERMINANTS AND PERMANENTS,
page 123,
equation (2.5.10) presently is
There is a missing parenthesis, this should have been:
(Thanks to Paul Stanford for this correction.)
This entry updated before 7 March 2001.
- Section 2.5.6,
SINGULARITY, RANK, AND INVERSES,
page 125,
item number 6,
- equation (2.5.16),
the formula for X is given incorrectly. It now has
X=(B-CE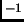 )
)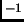
This is incorrect. It should have been (note the missing 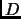 ):
):
X=(B-CE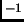 D)
D)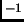
- The following should be added after equation (2.5.17)
The inverse of a 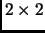 matrix is as follows
(defined when
matrix is as follows
(defined when 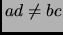 ):
):
This entry updated before 7 March 2001.
- Section 2.5.11,
GENERALIZED INVERSES,
page 129,
item number 2,
the statement is mostly incorrect. Presently we have
Only if  is square and non-singular,
is square and non-singular,
 will be
unique and
will be
unique and
 . Otherwise, there will exist
infinitely many matrices
. Otherwise, there will exist
infinitely many matrices
 that will satisfy the
defining relation.
that will satisfy the
defining relation.
This is incorrect. It should have been
There is a unique pseudoinverse satisfying the conditions in (2.5.26).
If, and only if,  is square and non-singular, then
is square and non-singular, then
 .
.
(Thanks to Pablo A. Parrilo for this correction.)
This entry updated before 7 March 2001.
- Section 2.5.17,
THEOREMS,
page 135,
equation (2.5.31) presently has (in part)
There are missing terms and missing ellipses, this should have been
(Thanks to Paul Stanford for this correction.)
This entry updated before 7 March 2001.
- Section 2.6.8,
PERMUTATION GROUPS,
pages 147-148,
the definition of the cycle index is missing. The following should be
included:
Suppose that 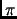 is a permutation with
is a permutation with
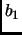 cycles of length
cycles of length 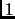 ,
,
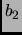 cycles of length
cycles of length 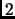 ,
...,
,
...,
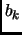 cycles of length
cycles of length 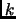 in its unique cycle decomposition.
Then
in its unique cycle decomposition.
Then 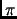 can be encoded as the expression
can be encoded as the expression
 .
Summing these expressions for all permutations in the group
.
Summing these expressions for all permutations in the group 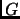 ,
and normalizing by the number of elements in
,
and normalizing by the number of elements in 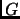 results in the
cycle index of the group
results in the
cycle index of the group 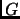 :
:
This entry updated before 7 March 2001.
- Section 3.2.3,
BINOMIAL COEFFICIENTS,
page 169,
the following text should be added
- If
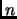 and
and 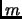 are integers, and
are integers, and 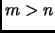 , then
, then
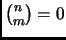
This entry updated before 7 March 2001.
- Section 3.2.3,
Pascal's triangle,
page 170,
the table now begins as
1
1 2 1
1 3 3 1
which is incorrect, it should have been
1
1 1
1 2 1
1 3 3 1
(Thanks to Katherine Jane Harine for this correction.)
This entry last updated 25 Februrary 2002.
- Section 3.2.9,
STIRLING CYCLE NUMBERS,
page 174,
the displayed expression is
This is incorrect. It should say (note
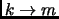 )
)
There are also several other small errors in sections 3.2.8 and 3.2.9.
(Thanks to David Jeffrey for pointing out many errors.)
This entry last updated 5 October 2001.
- Section 3.5.7,
LATIN SQUARES,
page 214,
the
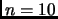 Latin square has as its fourth row
Latin square has as its fourth row
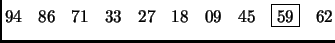
This is incorrect. This row should have been (look at second to last element)

This entry updated before 7 March 2001.
- Section 3.7.4,
BINARY SEQUENCES,
page 225,
table at the top of the page
- The sequence marked with a ``7 S'' in the first column should be
marked by a ``7''.
- The third sequence marked by a ``7'' in the first column should
be marked by a ``7 S''.
(Thanks to Joe Rushanan for these corrections.)
This entry updated before 7 March 2001.
- Section 4.5.13,
REGULAR POLYGONS,
page 276,
in the first set of displayed equations:
- the expression ``area=
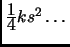 '' should have been
``area=
'' should have been
``area=
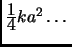 ''
''
- the expression ``
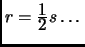 '' should have been
``
'' should have been
``
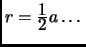 ''
''
- the expression ``
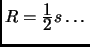 '' should have been
``
'' should have been
``
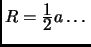 ''
''
(Thanks to L. W. Maxwell for this correction.)
This entry updated before 7 March 2001.
- Section 4.6,
CIRCLES,
page 277,
just before the last sentence add on the page, add the text
(All angles are measured in radians.)
This entry updated before 7 March 2001.
- Section 4.7.1,
ALTERNATIVE CHARACTERIZATION,
page 281,
last line, the eccentricity is currently written as
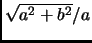
This is incorrect. It should have been
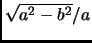
(Thanks to Gary E. Young for this correction.)
This entry updated before 7 March 2001.
- Section 4.7.3,
ADDITIONAL PROPERTIES OF ELLIPSES,
page 285,
at the end of note number 1,
the following text should be added:
Note the approximation
![$ C \approx
2a\left[ 2+(\pi-2)\left( \frac{b}{a} \right)^{1.456} \right]$](smtf30_p2_img104.png)
(Thanks to David F. Rivera for this addition.)
This entry updated before 7 March 2001.
- Section 4.7.3,
ADDITIONAL PROPERTIES OF ELLIPSES,
page 285
- First displayed equation, below and to the left of the figure,
the rightmost expression is presently
This is incorrect, it should have been
- On the next line we present have
Setting
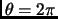
This is incorrect, it should have been
Setting
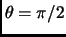
- In the next display, the rightmost expression is presently
This is incorrect, it should have been
(Thanks to David Cantrell for these corrections.)
This entry updated before 7 March 2001.
- Section 4.8.2,
ROULETTES (SPIROGRAPH CURVES)
page 292,
the second displayed equation is now
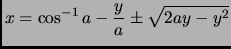
This is incorrect. It should say (note 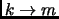 )
)
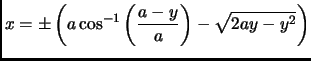
(Thanks to James Seed for this correction.)
This entry updated before 7 March 2001.
- Section 4.8.3,
SPIRALS,
page 294,
the first full sentence is now
A curve parameterized by arclength and such that the curvature is
proportional to the parameter at each point is a Bernoulli spiral.
This is incorrect. It should say
A curve parameterized by arclength and such that the radius of
curvature is proportional to the parameter at each point is a
Bernoulli spiral.
This entry updated before 7 March 2001.
- Section 4.8.3,
SPIRALS,
page 294,
the last sentence is now
A curve parameterized by arclength and such that the curvature is
inversely proportional to the parameter at each point is a Cornu
spiral (compare the Bernoulli spiral).
This is incorrect. It should say
A curve parameterized by arclength and such that the radius of
curvature is inversely proportional to the parameter at each point
is a Cornu spiral (compare the Bernoulli spiral).
This entry updated before 7 March 2001.
- Section 4.10,
SPACE SYMMETRIES OR ISOMETRIES,
page 300,
- Line 5 now has ``in a line
 '', which is incorrect.
It should have been ``in a plane
'', which is incorrect.
It should have been ``in a plane  ''.
''.
- Line 6 now has ``in a line
 '', which is incorrect.
It should have been ``in a plane
'', which is incorrect.
It should have been ``in a plane 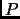 ''.
''.
- An additional line, (number 7), should be added. It should say
A rotation-reflection (rotation through an angle 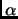 around a line
around a line 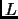 composed with reflection in a plane
perpendicular to
composed with reflection in a plane
perpendicular to 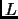 ).
).
(Thanks to Jerry Grossman for these corrections.)
This entry updated before 7 March 2001.
- Section 4.15.1,
REGULAR POLYHEDRA,
page 311,
the
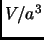 ratio for the Dodecahedron is now listed as
ratio for the Dodecahedron is now listed as
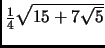 7.663119
7.663119
This is incorrect. It should have been
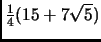 7.663119
7.663119
(Thanks to David G. Simpson for this correction.)
This entry updated before 7 March 2001.
- Section 4.18,
SPHERES,
page 314,
line 9, now has
Four points not on the same  ...
...
This is incorrect. It should have been
Four points not on the same  ...
...
This entry updated before 7 March 2001.
- Section 4.18,
SPHERES,
page 315,
equation 4.18.2,
now has

![$ \displaystyle
S_n(r)=\frac{n}{r} V_n = \frac{d }{d r} [V_n(r)]$](smtf30_p2_img122.png)
This is correct, but could be clarified by writing it as:
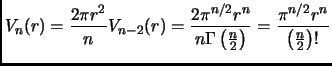
![$ \displaystyle
S_n(r)=\frac{n}{r} V_n(r) = \frac{d }{d r} [V_n(r)]$](smtf30_p2_img124.png)
(Thanks to Randolph J. Herber for this clarification.)
This entry updated before 7 March 2001.
- Section 5.1,
DIFFERENTIAL CALCULUS,
page 335,
last formulae on the page is now
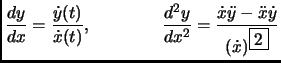
This is incorrect. It should have been
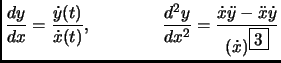
(Thanks to Richard W. Johnson for this correction.)
This entry last updated 20 September 2001.
- Section 5.1.1,
MAXIMA AND MINIMA OF FUNCTIONS,
page 338,
lines 4-6 are now
The solutions are:
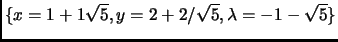 (furthest), and
(furthest), and
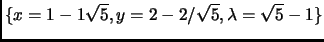 (closest).
(closest).
These are incorrect. They should have been (note the last equation on
the first line is missing a ``1'', and a slash is missing in the two
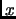 solutions):
solutions):
The solutions are:
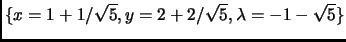 (furthest), and
(furthest), and
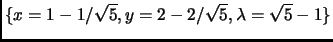 (closest).
(closest).
(Thanks to Bruno Van der Bossche for these corrections.)
This entry updated before 7 March 2001.
- Section 5.1.3,
PROPERTIES,
page 340,
item number 4 now has
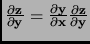
This is incorrect. It should have been
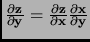
(Thanks to Pablo A. Parrilo for this correction.)
This entry updated before 7 March 2001.
- Section 5.3.5,
Useful transformations,
page 349,
items 4 and 5 now have
when
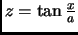
This is incorrect. It should have been
when
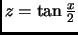
This entry last updated 25 Februrary 2002.
- Section 5.3.13,
ASYMPTOTIC INTEGRAL EVALUATION,
page 357,
last line on the page,
we presently have
![$\displaystyle \sim g(x_0) \sqrt{ \frac{2\pi}{\lambda \left\vert f''(x_0)\right\...
...} \left[ i\lambda f(x_0) -\frac{i\pi}{4}\,\hbox{signum}f''(x_0) \right] + \dots$](smtf30_p2_img137.png) |
(5.3.21) |
This is incorrect, it should have been
(note that the exponential function is missing, and that the last sign
is incorrect)
![$\displaystyle \sim g(x_0) \sqrt{ \frac{2\pi}{\lambda \left\vert f''(x_0)\right\...
... \left[ i\lambda f(x_0) + \frac{i\pi}{4}\,\hbox{signum}f''(x_0) \right] + \dots$](smtf30_p2_img138.png) |
(5.3.21) |
(Thanks to Richard B. Evans for these corrections.)
This entry updated before 7 March 2001.
- Section 5.3.14,
MOMENTS OF INERTIAL FOR VARIOUS BODIES,
page 358,
entry number 12 which is for a ``spherical shell, very thin, mean
radius
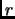 '' the moment of inertia is listed as
'' the moment of inertia is listed as
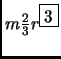
This is incorrect, it should have been
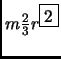
(Thanks to Richard Finley for this correction.)
This entry updated before 7 March 2001.
- Section 5.4.8,
FORMS CONTAINING
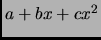 ,
page 367,
the second line is now
,
page 367,
the second line is now
If  , then
, then
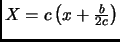 and other formulae
should be used.
and other formulae
should be used.
This is incorrect, it should have been
If  , then
, then
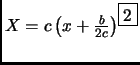 and
other formulae should be used.
and
other formulae should be used.
This entry last updated 25 Februrary 2002.
- Section 5.4.11,
FORMS CONTAINING
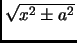 ,
pages 370-371,
integrals number 149, 150, 161, and
164 all have the expression
,
pages 370-371,
integrals number 149, 150, 161, and
164 all have the expression
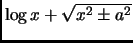
This is incorrect, it should have been
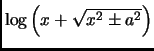
(Thanks to Jonathan Thomas Bartley for these corrections.)
This entry updated before 7 March 2001.
- Section 5.4.12,
FORMS CONTAINING
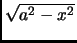 ,
page 373,
integral number 208 is missing the
,
page 373,
integral number 208 is missing the 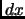
(Thanks to Guizhong Zhang for this correction.)
This entry updated before 7 March 2001.
- Section 5.5,
TABLE OF DEFINITE INTEGRALS,
- page 396,
integral number 586 is presently:
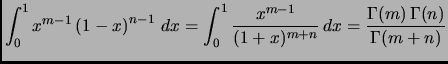
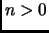 ,
, 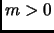 .
.
This is incorrect and should be
(note the upper limit on the second integral):
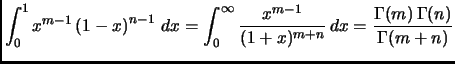
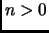 ,
, 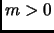 .
.
- page 397,
integral number 598 is presently:
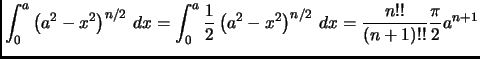 ,
,
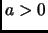 ,
, 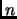 is an odd integer.
is an odd integer.
This is incorrect and should be
(note the lower limit on the second integral):
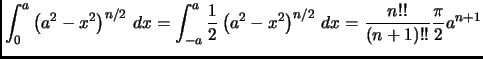 ,
,
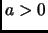 ,
, 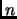 is an odd integer.
is an odd integer.
- page 398,
integral number 606 is presently:
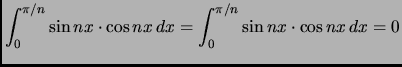 ,
, 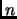 is an integer.
is an integer.
This is correct but should have been
(note the upper limit on the second integral):
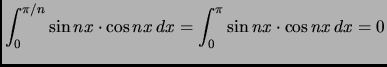 ,
, 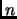 is an integer.
is an integer.
FOOTNOTE: An alert reader will wonder how these errors could have
occurred, since the integrals in the 30th edition of this book have
been electronically verified. The error occurred in the typesetting of
the integrals--not in the electronic verification of the integrals.
In this section on definite integrals, there are 11 integrals in which
there were two integrals on the same line; in all cases the limits on
the first integral were (sometimes incorrectly) printed as the limits
on the second integral. This resulted in the errors listed above.
(Thanks to Michael Strauss for this correction.)
This entry updated before 7 March 2001.
- Section 5.5,
TABLE OF DEFINITE INTEGRALS,
page 400,
integral number 646 presently has ``
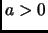 ''.
This statement is not needed since
''.
This statement is not needed since 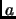 does not appear in the integral.
does not appear in the integral.
(Thanks to Luke Sweatlock for this correction.)
This entry last updated 25 Februrary 2002.
- Section 5.5,
TABLE OF DEFINITE INTEGRALS,
page 400,
integral number 648 presently has ``
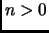 ''.
This is incorrect, it should have been ``
''.
This is incorrect, it should have been ``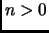 and
and 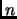 even''.
even''.
(Thanks to Luke Sweatlock for this correction.)
This entry last updated 25 Februrary 2002.
- Section 5.7.8,
SEPARATION OF VARIABLES,
on page 423,
- line 6, now has
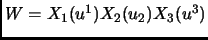
This is incorrect. It should have been

- line 6, fourth displayed equation is now
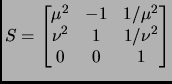 ,
,
This is incorrect. It should have been
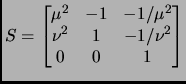 ,
,
- line 14, now has
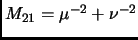
This is incorrect. It should have been (note the subscript)
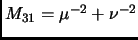
- line 15, now has
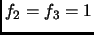 .
.
This is incorrect. It should have been
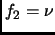 , and
, and 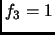 .
.
- fifth displayed equation is now (in part)
This is incorrect. It should have been
This entry updated before 7 March 2001.
- Section 5.10.3,
DIFFERENTIATION OF TENSORS,
page 433,
equation (5.10.8), we presently have
This is incorrect. It should have been (notice that the second superscript
on the second line has an 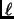 that should be an
that should be an 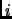 )
)
(Thanks to Harry Watson of the Naval Warfare Assessment Division
(NWAD) for this correction.)
This entry updated before 7 March 2001.
- Section 5.11.1,
LIST OF ORTHGONAL COORDINATE SYSTEMS,
pages 442-445,
each formula of the form ``
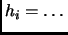 '' should have instead been
``
'' should have instead been
``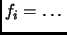 ''.
''.
This entry updated before 7 March 2001.
- Section 5.12,
CONTROL THEORY,
page 445,
the derivative on the
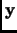 term in the second equation is incorrect,
the definition of controllability is incorrect, and the
controllability and observability criteria should be be stated as ``if
and only if''. Also, the statements could be made in more generality.
The first three paragraphs of this section should be replaced by:
term in the second equation is incorrect,
the definition of controllability is incorrect, and the
controllability and observability criteria should be be stated as ``if
and only if''. Also, the statements could be made in more generality.
The first three paragraphs of this section should be replaced by:
Let 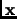 be a state vector, let
be a state vector, let 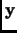 be an observable vector,
and let
be an observable vector,
and let 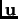 be the control. The vectors
be the control. The vectors 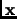 ,
, 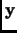 , and
, and
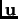 have
have 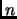 ,
, 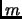 and
and 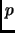 components, respectively.
If a system evolves as:
components, respectively.
If a system evolves as:
then, taking Laplace transforms,
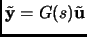 where
where 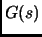 is the transfer function given by
is the transfer function given by
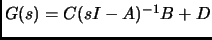 .
.
A system is said to be controllable if and only if for any times
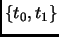 and any states
and any states
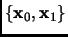 there exists a
control
there exists a
control
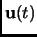 such that
such that
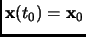 and
and
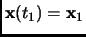 . The system is controllable if and only if rank
. The system is controllable if and only if rank
![$ [B\ AB\
A^2B\ \dots \ A^{n-1}B]=n$](smtf30_p2_img196.png) .
.
If, given
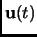 and
and
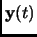 on some interval
on some interval 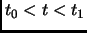 ,
the value of
,
the value of
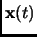 can be deduced on that interval, then the
system is said to be observable. Observability is equivalent to the
condition rank
can be deduced on that interval, then the
system is said to be observable. Observability is equivalent to the
condition rank
![$ [C^{\rm T}\ A^{\rm T}C^{\rm T}\ \dots\
\left( A^{(n-1)} \right) ^{\rm T}C^{\rm T}]=n$](smtf30_p2_img200.png) .
.
(Thanks to Pablo A. Parrilo for this correction.)
This entry updated before 7 March 2001.
- Section 6.1.9,
CIRCULAR FUNCTIONS OF SOME SPECIAL ANGLES,
page 455,
there are two errors:
- The sine of 120
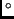 is
is
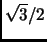 (and not
(and not 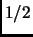 )
)
- The sine of 150
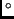 is
is 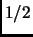 (and not
(and not
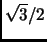 )
)
(Thanks to Andre D. Bandrauk for these corrections.)
This entry updated before 7 March 2001.
- Section 6.1.14,
DOUBLE ANGLE FORMULAE,
page 458,
in the sine double angle formula (the first formula),
the
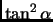 term in the denominator has an incorrect factor of
2. It now has:
It should have been
term in the denominator has an incorrect factor of
2. It now has:
It should have been
(Thanks to Richard F. Stein for this correction.)
This entry updated before 7 March 2001.
- Section 6.2.2,
GENERAL PLANE TRIANGLES
page 461,
``Triangle sides in terms of other components",
presently has
This is incorect, it should have been
(Thanks to Richard Hughes for this correction.)
This entry last updated 25 Februrary 2002.
- Section 6.4,
SPHERICAL SPHERICAL TRIANGLES
page 468.
Figure 6.4.3 and the first line of ``Napier's rules of cicrular parts''
both presently have ``co-
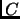 ''. This is incorrect,it should have been
``co-
''. This is incorrect,it should have been
``co-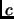 ''.
''.
(Thanks to Donal M. Ragan for this correction.)
This entry last updated 25 Februrary 2002.
- Section 6.10.11,
TABLE OF SPHERICAL HARMONICS,
page 493,
the
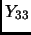 term is presently
term is presently
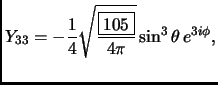
This is incorrect. It should have been

(Thanks to William Weintraub for this correction.)
This entry last updated 20 September 2001.
- Section 6.17.3,
POLYNOMIAL CASE,
page 510,
now has (in part)
This is incorrect. It should have been (notice that
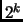 is replaced
by
is replaced
by 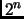 ):
):
(Thanks to Michael E. Kutz for this correction.)
This entry updated before 7 March 2001.
- Section 6.19.3,
COMPLEMENTARY INTEGRALS,
page 523,
now has
This is incorrect. It should have been (notice the order of the arguments)
(Thanks to David W. Cantrell for this correction.)
This entry updated before 7 March 2001.
- Section 6.30,
TABLES OF TRANSFORMS,
page 559,
Laplace transforms: functional relations,
number 12,
now has
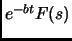
This is incorrect. It should have been
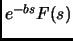
(Thanks to David Lassonde for this correction.)
This entry updated before 7 March 2001.
- Section 6.30,
TABLES OF TRANSFORMS,
page 563,
Laplace transforms,
number 74,
now has
This is incorrect. It should have been
(Thanks to Dale Hinds for this correction.)
This entry last updated 20 September 2001.
- Section 7.1.8,
GEOMETRIC PROBABILITY,
page 579,
- number 2,
the first displayed equation is now
This is incorrect, it should have been (note that ``1'' should have
been a ``k'' in one of the binomial coefficients)
- number 5 (Buffon's needle problem) presently has
A needle of length 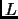 is placed at random on a plane on which are
ruled parallel lines at unit distance apart. Assume that
is placed at random on a plane on which are
ruled parallel lines at unit distance apart. Assume that 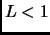 so
that only one intersection is possible. The probability
so
that only one intersection is possible. The probability 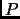 that
the needle intersects a line is
that
the needle intersects a line is
This is incorrect and incomplete (the
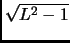 should have been
should have been
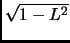 ). It should have been:
). It should have been:
A needle of length 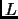 is placed at random on a plane on which are
ruled parallel lines a distance
is placed at random on a plane on which are
ruled parallel lines a distance 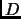 apart. If
apart. If
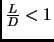 then
only one intersection is possible. The probability
then
only one intersection is possible. The probability 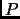 that the
needle intersects a line is
that the
needle intersects a line is
This entry updated before 7 March 2001.
- Section 7.2.1,
DISCRETE DISTRIBUTIONS,
page 582,
number 5,
Negative Binomial Distribution,
now has
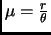
and
![$ G(t)=e^{tr}\theta^r[1-(1-\theta)e^t]^{-r}$](smtf30_p2_img234.png)
They are both incorrect. They should have been
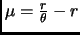
and
![$ G(t)=\theta^r[1-(1-\theta)e^t]^{-r}$](smtf30_p2_img236.png)
(Thanks to Dillard David Ensley for this correction.)
This entry updated before 7 March 2001.
- Section 7.2.2,
CONTINUOUS DISTRIBUTIONS,
page 583,
note number 2,
Normal Distribution,
now has
then the variable 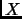 is said to possess a uniform distribution
is said to possess a uniform distribution
This is incorrect. It should have been
then the variable 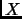 is said to possess a normal distribution
is said to possess a normal distribution
(Thanks to Ian M. Dew of Pacific-Sierra Research Corp. for this correction.)
This entry updated before 7 March 2001.
- Section 7.2.2,
CONTINUOUS DISTRIBUTIONS,
page 586,
part 9,
Student's t-distribution,
equation (7.2.32) presently has
This should have been (note that
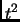 should be
should be 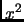 ):
):
(Thanks to Paul Stanford for this correction.)
This entry updated before 7 March 2001.
- Section 7.4.1,
TRANSITION FUNCTION,
page 589,
line 4,
we presently have
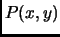 is the probability that a Markov chain in state
is the probability that a Markov chain in state 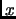 at
time
at
time 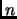 will be in state
will be in state 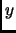 at time
at time 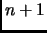 .
.
This is incorrect. It should have been
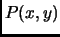 is the probability that a Markov chain in state
is the probability that a Markov chain in state 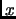 at
time
at
time 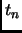 will be in state
will be in state 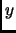 at time
at time 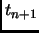 .
.
(Thanks to Harry Watson of the Naval Warfare Assessment Division
(NWAD) for this correction.)
- Section 7.4.2,
TRANSITION MATRIX,
page 590,
top of page,
we presently have
Define the 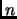 -step transition matrix by
-step transition matrix by
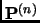 as the matrix with entries
as the matrix with entries
This is incorrect. It should have been
Define the 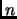 -step transition matrix by
-step transition matrix by
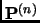 as the matrix with entries
as the matrix with entries
(Thanks to Harry Watson of the Naval Warfare Assessment Division
(NWAD) for this correction.)
This entry updated before 7 March 2001.
- Section 7.4.4,
STATIONARY DISTRIBUTIONS,
page 592,
the matrix at the top of the page is incorrect.
We presently have
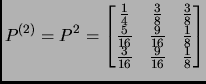
This is incorrect, it should have been
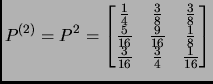
(Thanks to Dennis J. Day for this correction.)
This entry updated before 7 March 2001.
- Section 7.5.1,
METHODS OF PSEUDORANDOM NUMBER GENERATION,
page 594,
part 9,
second table on page, first table after equation (7.5.3) is
presently
| Primitive trinomial exponents |
| (5,2) |
(7,1) |
(7,3) |
(17,3) |
(17,5) |
(17,6) |
| (31,3) |
(31,6) |
(31,7) |
(31,13 |
(127,1) |
(521,32) |
This should have been (note the missing closing parenthesis for the 31-13 entry):
| Primitive trinomial exponents |
| (5,2) |
(7,1) |
(7,3) |
(17,3) |
(17,5) |
(17,6) |
| (31,3) |
(31,6) |
(31,7) |
(31,13) |
(127,1) |
(521,32) |
(Thanks to Paul Stanford for this correction.)
This entry updated before 7 March 2001.
- Section 7.5.2,
GENERATING NONUNIFORM RANDOM VARIABLES,
page 597,
line 4,
presently there is
This is incorrect. This should have been
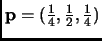
This entry updated before 7 March 2001.
- Section 7.7.4,
ORDER STATISTICS,
page 607,
we presently have
...let  be the
be the 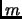 th largest of the values (
th largest of the values (
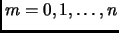 ).
Hence
).
Hence 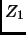 is the maximum of the
is the maximum of the 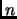 values and
values and 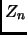 is the minimum
of the
is the minimum
of the 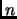 values. Then
values. Then
![$ \displaystyle
F_{Z_m}(x)= \sum_{m=1}^n \binom{n}{i}
\left[ F_X(x) \right]^i\left[ 1-F_X(x) \right]^{n-i}
$](smtf30_p2_img256.png) .
Hence
.
Hence
This is incorrect. It should have been (note 3 things: the range of
values, the definition for
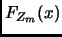 , and the subscripts in the
minimum and maximum densities):
, and the subscripts in the
minimum and maximum densities):
...let  be the
be the 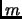 th largest of the values
(
th largest of the values
(
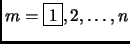 ). Hence
). Hence 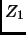 is the maximum of the
is the maximum of the 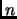 values and
values and 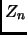 is the minimum of the
is the minimum of the 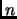 values. Then
values. Then
![$ \displaystyle
F_{Z_m}(x)= \sum_{\fbox{$i=m$}}^n \binom{n}{i}
\left[ F_X(x) \right]^i\left[ 1-F_X(x) \right]^{n-i}
$](smtf30_p2_img267.png) .
Hence
.
Hence
This entry updated before 7 March 2001.
- Section 7.8.1,
CONFIDENCE INTERVAL: SAMPLE FROM ONE POPULATION
page 609,
number 3,
bullet 4,
we presently have
...confidence interval for 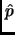 is given by ...
is given by ...
This is incorrect. It should have been
...confidence interval for 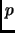 is given by ...
is given by ...
This entry updated before 7 March 2001.
- Section 7.13.3,
MATCHED FILTERING (WEINER FILTER),
page 660,
the name ``Weiner'' is incorrect; it should have been ``Wiener''.
(Thanks to Pablo A. Parrilo for this correction.)
This entry updated before 7 March 2001.
- Section 8.1.4,
FITTING EQUATIONS TO DATA,
page 682,
Best fit line, now has
Given the points
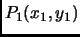 ,
,
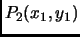 , ...
, ...
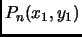 the ...
the ...
This is incorrect. It should have been (notice the subscripts)
Given the points
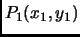 ,
,
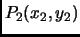 , ...
, ...
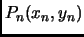 the ...
the ...
(Thanks to Harry Watson of the Naval Warfare Assessment Division
(NWAD) for this correction.)
This entry updated before 7 March 2001.
- Section 8.2.8,
NONLINEAR SYSTEMS AND NUMERICAL OPTIMIZATION,
page 691,
Method of steepest descent,
first displayed equation now ends
This is incorrect. It should have been (i.e., close the parenthesis)
(Thanks to Jeffrey D. Oldham for this correction.)
This entry updated before 7 March 2001.
- Section 8.3.1,
NUMERICAL INTEGRATION,
page 693,
Closed Newton-Cotes formulae,
number 3,
a closing square bracket is missing. That is, ``
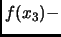 '' should
have been ``
'' should
have been ``![$ f(x_3)]-$](smtf30_p2_img281.png) ''.
''.
(Thanks to Pablo A. Parrilo for this correction.)
This entry updated before 7 March 2001.
- Section 8.3.1,
NUMERICAL INTEGRATION,
page 695,
the title Method H.2.1.2 Romberg Integration should have been
Romberg Integration.
This entry updated before 7 March 2001.
- Section 8.3.1,
NUMERICAL INTEGRATION,
page 695,
the following should be added:
Double integrals of polynomials over polygons
If the vertices of the polygon 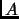 are
are
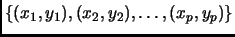 , and we define
, and we define
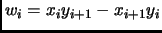 (with
(with
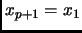 and
and
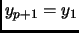 ) then
) then
(Thanks to Joaquin Marin for this addition.)
This entry updated before 7 March 2001.
- Section 9.1.3,
EXAMPLES
page 722,
- Question number 5, answer. The computation as stated is
correct, but the numerical evaluation was performed
incorrectly. The monthly payment is not $755.63, it should be
$804.62.
- Question number 6. The statement ``spending $600 per month''
should be changed to ``spending $800 per month''.
- Question number 6, analysis. The statement ``
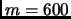 ''
should be changed to ``
''
should be changed to ``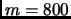 ''.
''.
This entry updated before 7 March 2001.
- Section 10.7.1,
CONTACT INFORMATION,
page 747,
note number 7, we presently have
Mathematica http://www.wri.com
While this works, a better reference is
Mathematica http://www.wolfram.com
(Thanks to David Gehrig for this correction.)
This entry updated before 7 March 2001.
- Section 10.10,
ASCII CHARACTER CODES,
page 755,
the table now has a heading of
American Standard Code for Information 
This is incorrect. It should have been
American Standard Code for Information 
(Thanks to Alex Fabrikant for this correction.)
This entry last updated 5 October 2001.
- List of Notations,
page 757,
the following should be added:
 is the floor function
(greatest integer less than or equal to the argument)
is the floor function
(greatest integer less than or equal to the argument)
 is the ceiling function
(least integer larger than or equal to than the argument)
is the ceiling function
(least integer larger than or equal to than the argument)
(Thanks to David Cantrell for this correction.)
This entry last updated 25 Februrary 2002.

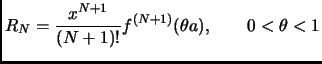

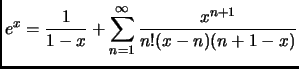
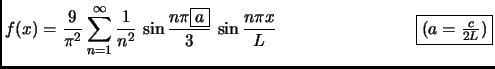

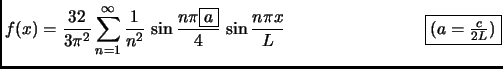
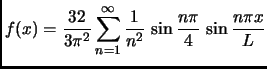
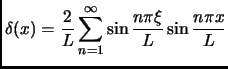 for
for 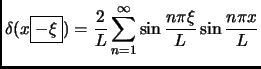 for
for 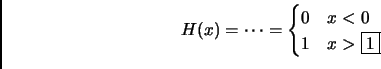 .
.
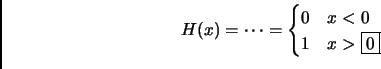 .
.
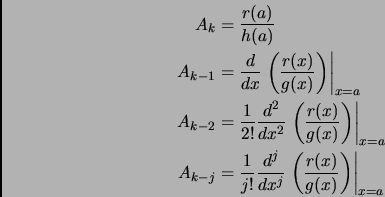
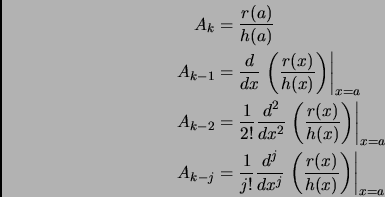
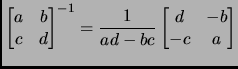

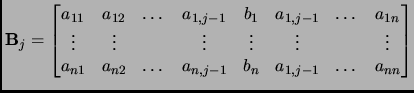
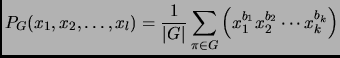
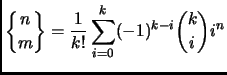
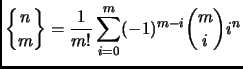
![$ C \approx
2a\left[ 2+(\pi-2)\left( \frac{b}{a} \right)^{1.456} \right]$](smtf30_p2_img104.png)
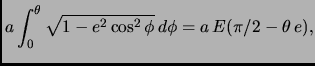
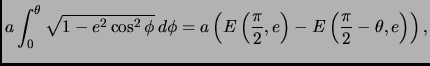
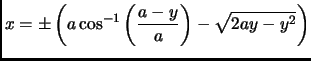

![$ \displaystyle
S_n(r)=\frac{n}{r} V_n = \frac{d }{d r} [V_n(r)]$](smtf30_p2_img122.png)
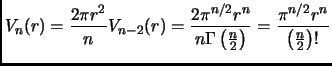
![$ \displaystyle
S_n(r)=\frac{n}{r} V_n(r) = \frac{d }{d r} [V_n(r)]$](smtf30_p2_img124.png)
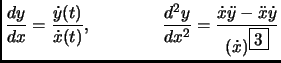
![$\displaystyle \sim g(x_0) \sqrt{ \frac{2\pi}{\lambda \left\vert f''(x_0)\right\...
...} \left[ i\lambda f(x_0) -\frac{i\pi}{4}\,\hbox{signum}f''(x_0) \right] + \dots$](smtf30_p2_img137.png)
![$\displaystyle \sim g(x_0) \sqrt{ \frac{2\pi}{\lambda \left\vert f''(x_0)\right\...
... \left[ i\lambda f(x_0) + \frac{i\pi}{4}\,\hbox{signum}f''(x_0) \right] + \dots$](smtf30_p2_img138.png)
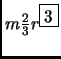
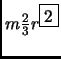
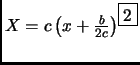 and
other formulae should be used.
and
other formulae should be used.
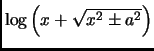
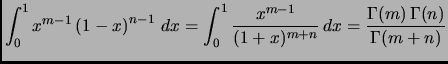
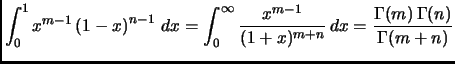
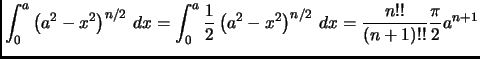 ,
,
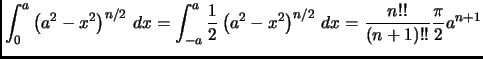 ,
,
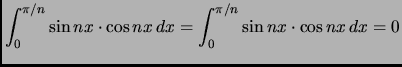 ,
, 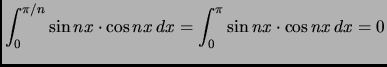 ,
, 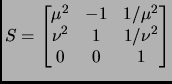 ,
,
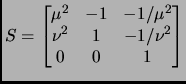 ,
,
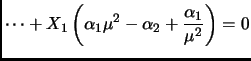
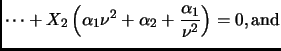
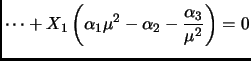
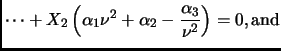
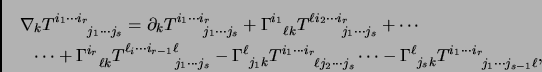
![$ [C^{\rm T}\ A^{\rm T}C^{\rm T}\ \dots\
\left( A^{(n-1)} \right) ^{\rm T}C^{\rm T}]=n$](smtf30_p2_img200.png) .
.
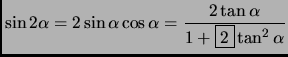

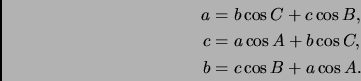
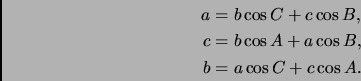
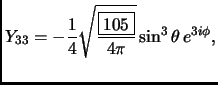

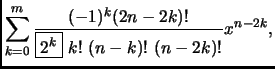
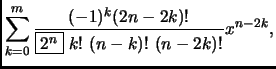
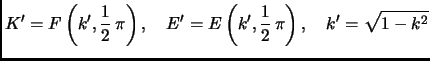
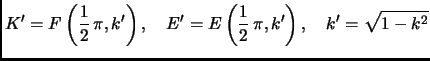
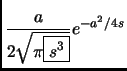

![\begin{displaymath}
\begin{aligned}
P_k(x)
&= \text{Probability (exactly $k$\ i...
...(-1)^s\binom{n-k}{s}[1-(k+s)x]^{n-1} \bigg\} \\
\end{aligned}\end{displaymath}](smtf30_p2_img226.png)
![$\displaystyle P=\frac{2}{\pi}\left[ \frac{\pi}{2}-\arcsin L^{-1}+L-\sqrt{L^2-1} \right]
$](smtf30_p2_img228.png)
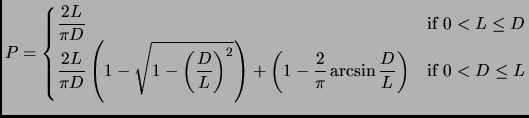
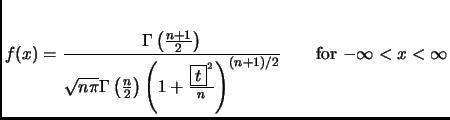
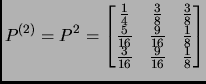
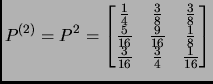
![$ \displaystyle
F_{Z_m}(x)= \sum_{m=1}^n \binom{n}{i}
\left[ F_X(x) \right]^i\left[ 1-F_X(x) \right]^{n-i}
$](smtf30_p2_img256.png) .
Hence
.
Hence
![$ \displaystyle
F_{Z_m}(x)= \sum_{\fbox{$i=m$}}^n \binom{n}{i}
\left[ F_X(x) \right]^i\left[ 1-F_X(x) \right]^{n-i}
$](smtf30_p2_img267.png) .
Hence
.
Hence