This file contains:
(1) a list of slide titles (hyperlinked), and
(2) the contents of each slide.
A pdf version of the talk is
available here
Sudbury 1-1-623
telephone 978-440-1660
Daniel_I_Zwillinger@raytheon.com
http://www.mathtable.com/zwillinger/talks/20010613/
This course will expose users to the Matlab software language. The language will be described at a high level. Matlab's capabilities (data types, programming constructs, functions, toolboxes, and graphics) and how users tend to use them will be discussed. A discussion of when to use Matlab will be given. A demonstration will be given.
``Like every other scripting language, Matlab began as a simple way to do powerful things, and it has become a not-so-simple way to do very powerful things.''
2
![]()
![]()
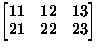
>> A=zeros(2,2)
A =
0 0
0 0
>> B=ones(3,2)
B =
1 1
1 1
1 1
>> C=eye(3)
C =
1 0 0
0 1 0
0 0 1
>> D=[1 2; 3 4]
D =
1 2
3 4
>> s= 1:4
s =
1 2 3 4
>> s2= 1:2:7
s2 =
1 3 5 7
>> s3= 1:.5:2
s3 =
1.0000 1.5000 2.0000
>> r=rand(2,3) r = 0.47 0.85 0.20 0.42 0.53 0.67 >> r(:,1) ans = 0.47 0.42 >> r(:,1)' ans = 0.47 0.42
>> A=zeros(2,2);
>> B=ones(3,2);
>> C=[ [A;B], [B+5;A-7] ]
C =
0 0 6 6
0 0 6 6
1 1 6 6
1 1 -7 -7
1 1 -7 -7
>> C(:,[1 4])
ans =
0 6
0 6
1 6
1 -7
1 -7
>> log( 1 )
ans =
0
>> log( [1 2] )
ans =
0 0.6931
>> log( [1 2; 0 NaN] )
Warning: Log of zero.
ans =
0 0.6931
-Inf NaN
| Input | Output | |
| u<3 | [1 1 0] | |
| all(u<3) | 0 | |
| any(u<3) | 1 | |
| find(u<3) | [1 2] |
>> a = eye(4) + 0.01*rand(4,4)
a =
1.0095 0.0089 0.0082 0.0092
0.0023 1.0076 0.0044 0.0074
0.0061 0.0046 1.0062 0.0018
0.0049 0.0002 0.0079 1.0041
>> eig(a)
ans =
1.0232
1.0009 + 0.0046i
1.0009 - 0.0046i
1.0023
x=inv(A) * b
or
[L,U,P]=lu(A)
x=inv(U) * inv(L) * P * b
or
x=A![]() b
b
or
...
>> A=rand(3,2)
A =
0.7095 0.1897
0.4289 0.1934
0.3046 0.6822
>> b=rand(3,1)
b =
0.3028
0.5417
0.1509
>> soln=A\b
soln =
0.6387
-0.0121
![]() Sparse matrices
Sparse matrices
>> A=speye(100000,100000);
>> A2=2*A;
>> A2(4,5)=5;
>> nnz(A2)
ans =
100001
![]() Multidimensional arrays
Multidimensional arrays
>> r=rand(2,2,3)
r(:,:,1) =
0.1389 0.1987
0.2028 0.6038
r(:,:,2) =
0.2722 0.0153
0.1988 0.7468
r(:,:,3) =
0.4451 0.4660
0.9318 0.4186
>> i=0;
>> for t=0:0.001:10
i=i+1;
y(i)=sin(t);
end
>> time1=toc
time1 =
0.1936
>> t=0:0.001:10;
>> y=sin(t);
>> time2=toc
time2 =
0.0111
>> time1/time2
ans =
17.4677
| ans | most recent result |
| eps | machine epsilon |
| flops | total floating point ops during session |
| i,j | |
| inf | |
| NaN | not-a-number |
| pi | |
| realmax | largest positive floating point number |
| realmin | smallest positive floating point number |
>> x=0:.1:10; >> y=sin(x); >> plot(x,y)
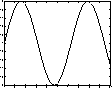
>> data=[2 6 4];
>> text={'a','b','c'};
>> pie(data,text)
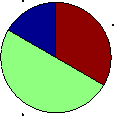
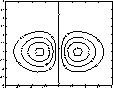
>> [X,Y]=...
meshgrid(-2:.2:2,-2:.2:3);
>> Z = X.*exp(-X.^2-Y.^2); >> [C,h] = contour(X,Y,Z); >> clabel(C,h)
>> t=0:.1:10; >> x=sin(t); >> y=cos(t); >> z=x'*y; >> meshc(x,y,z);

>> format + >> A=random(5,15)-1/2 A = ++--+++-+++++-+ +-+---+-++-+++- -++--+-+--+-+-- +-+--+---+++--- -+-++-----+--+-
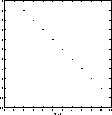
>> B=zeros(10,10) >> for i=1:9 >> B(i,i+1)=2; >> end >> spy(B)

![\fbox {\begin{minipage}
{0.98in}
\texttt{function e=foo(f,g)}\\ $\vdots$\\ \texttt{[h,i]=bar(f)}
\\ $\vdots$\\ \texttt{e=sqrt(h)}
\end{minipage}}](matlab_img18.gif)
![\fbox {\begin{minipage}
{1.19in}
\texttt{function [j,k,l]=bar(m)}\\ $\vdots$\space \\ \texttt{j=m} \\ \texttt{k=2*m}\\ \texttt{l=m*m}
\end{minipage}}](matlab_img19.gif)
![]() Have variables nargin and nargout
Have variables nargin and nargout
![]() Frequently have many short files
Frequently have many short files
GNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with Matlab. It may also be used as a batch-oriented language.
Octave has extensive tools for solving common numerical linear algebra problems ...It is easily extensible and customizable via user-defined functions written in Octave's own language, or using dynamically loaded modules written in C++, C, Fortran, or other languages.
GNU Octave is also freely redistributable software. You may redistribute it and/or modify it under the terms of the GNU General Public License (GPL) as published by the Free Software Foundation.