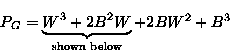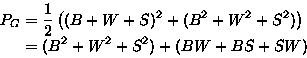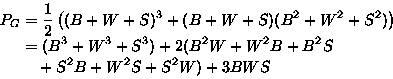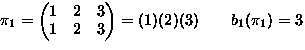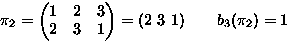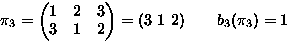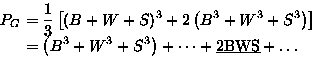Talk by Daniel Zwillinger
Raytheon
5 April 2001
This file contains:
(1) a list of slide titles (hyperlinked), and
(2) the contents of each slide.
A pdf version of the talk is
available here
-
Polya theory
-
Abstract
-
Outline
-
Daniel Zwillinger
-
Combinatorial problems
-
Sample selection
-
Balls into cells
-
Example: Switching functions (I)
-
Example: Switching functions (II)
-
Example: Radar filtering (I)
-
Example: Radar filtering (II)
-
Example: Radar filtering (III)
-
Example: Radar filtering (IV)
-
Counting transition diagrams
-
Permutation groups: Fast review
-
Permutation groups: Example
-
Burnside's Lemma
-
Example: 4-bead necklaces
-
Example: Necklaces with colored beads (I)
-
Example: Necklaces with colored beads (II)
-
Example: Rotations of an equilateral triangle
-
Example: Rotations of an equilateral triangle with colored beads (I)
-
Example: Rotations of an equilateral triangle with colored beads (II)
-
Special case of Polya's Theorem
-
Example: Necklaces with colored beads (III)
-
Example: Necklaces with colored beads (IV)
-
Example: Rotations of an equilateral triangle with colored beads (III)
-
Permutation groups: Cycle index
-
Polya's Theorem
-
Example: Necklaces with colored beads (V a)
-
Example: Necklaces with colored beads (V b)
-
Example: Necklaces with colored beads (V c)
-
Example: Necklaces with colored beads (V d)
-
Example: Necklaces with colored beads (V e)
-
Example: Rotations of an equilateral triangle with colored beads (IV)
-
Conclusion
-
References
(With a radar application motivation)
Daniel Zwillinger, PhD
5 April 2001
Sudbury 1-1-623
telephone 4-1660
Daniel_I_Zwillinger@raytheon.com
http://www.az-tec.com/zwillinger/talks/20010405/
http://nesystemsengineering.rsc.ray.com/training/memo.polya.pdf
This lecture will show how Polya theory can be used in counting
objects, which is often the design basis for statistical tests.
Specifically, Polya theory determines the number of distinct
equivalence classes of objects. It can also give counts for specific
types of patterns within equivalence classes. While sounding
esoteric, this simple-to-apply technique easily counts non-isomorphic
(i.e., different) graphs, and many other combinatorial structures. An
application to radar filtering of hard-limited data will be used to
motivate the topic.
- Introduction
- Who am I? Why am I talking?
- Talk is about combinatorial counting method
- Problem motivation
- Switching functions
- Radar filtering
- Necklaces:
using 3 beads of 3 different colors,
how many different necklaces are there?
- Polya theory
- Permutation groups
- Burnside's Lemma
- Education: MIT, Caltech
- Joined Raytheon in 2001 (Sr Principal Engineer)
- Formerly at: RPI,
JPL, BBN, IDA, MITRE,
Exxon,
Sandia Labs,
Ironbridge Networks,
consulting
- Broad expertise in applied mathematics
(continuous and discrete)
- Books on:
differential equations,
statistics,
integration methods,
table of integrals
- Editor-in-chief of
 edition of CRC's
Standard Mathematical Tables and Formulae
edition of CRC's
Standard Mathematical Tables and Formulae
- Home page: http://www.az-tec.com/zwillinger
- Combinatorial optimization
- How to define a problem?
- How many solutions are there?
- How to identify the solutions?
- How to find the best solution?
- Today's focus is on the number of solutions
- Standard counting problems (next 2 slides)
- Generating functions
- Standard problems (assignment problem, etc.)
- Polya theory
Choosing a sample of size r from m objects
| Repetitions allowed? |
Order counts? |
The sample is called an |
Number of ways to choose the sample |
| No |
No |
r-combination |
C(m,r) |
| No |
Yes |
r-permutation |
P(m,r) |
| Yes |
No |
r-combination with replacement |
CR(m,r) |
| Yes |
Yes |
r-permutation with replacement |
PR(m,r) |
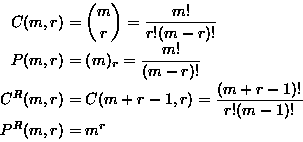
| Distinguish the cells |
Distinguish the balls |
Can cells be empty |
Number of ways to place n balls into k cells |
| Yes |
Yes |
Yes |
kn |
| Yes |
Yes |
No |
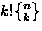 |
| Yes |
No |
Yes |
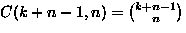 |
| Yes |
No |
No |
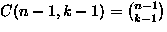 |
| No |
Yes |
Yes |
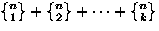 |
| No |
Yes |
No |
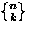 |
| No |
No |
Yes |
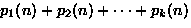 |
| No |
No |
No |
pk(n) |
-
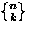 is a Stirling cycle number
is a Stirling cycle number
- pk(n) is the number of partitions of n into k parts
- A switching function (Boolean function) assigns a 0 or 1 to each
bit string of length n
- There are 22n different switching functions
(For n=4 have 65,536 switching functions)
- Allowing symmetries, there are
only 3,984 different switching functions (see [2])!
- Allowing an inverter and symmetries, there are
only 222 different switching functions (see [2])!
- Polya theory easily gives the number 222.
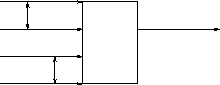
- D be a ``detection'', N is a ``no detection''
- R is a ``report'', ``-'' is ``no report''
- Sample filter result for ``2 out of 3'' filter

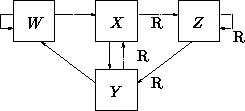
- ``2 out of 3'' filter has 4 states:
- State ``W'', last two input elements are ``NN''
- State ``X'', last two input elements are ``ND''
- State ``Y'', last two input elements are ``DN''
- State ``Z'', last two input elements are ``DD''
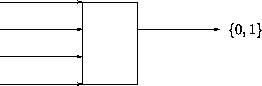
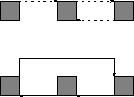
Transition diagram is
``N'' is shown as a solid line
``D'' is shown as a dashed line
- For iid inputs (D has a probability of p) have transition matrix
From state
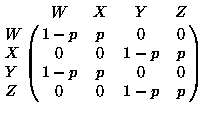
- Usual eigen-analysis yields steady state distribution:
| state |
W |
X |
Y |
Z |
| probability |
(1-p)2 |
p(1-p) |
p(1-p) |
p2 |
-
Need to know the number of directed graphs with out-degree one for different
numbers of vertices.
- Find (using Polya theory)
| number of states S |
2 |
3 |
4 |
| naive counting S2S |
16 |
729 |
65536 |
| number of actual filters |
10 |
129 |
2836 |
-
Use Sloane [4] to identify sequence A054050:
 10, 129, 2836, 83061, 3076386,
136647824, ...
10, 129, 2836, 83061, 3076386,
136647824, ... :``Number of non-isomorphic binary n-state automata''
[5]
:``Number of non-isomorphic binary n-state automata''
[5]
- Consider permutations of
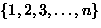
-
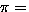
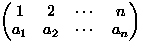
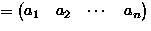
means
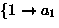 ,
,
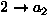 ,...,
,...,
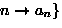 .
. -
Operation:
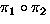 means: permute by
means: permute by 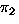 then by
then by 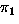
-
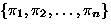 can be closed to form a group G
can be closed to form a group G
- ``a'' is invariant if
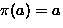 ; ``
; ``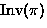 '' is number of elements invariant under
'' is number of elements invariant under 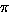
- Write
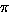 as unique product of disjoint cycles;
``
as unique product of disjoint cycles;
``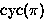 '' is number of cycles in
'' is number of cycles in 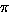
- An equivalence relation S (on G) is defined by ``
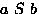 ''
iff there exists a
''
iff there exists a 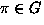 such that
such that 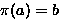
If 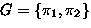 with
with
Then
If
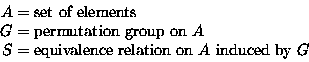
Then the number of equivalence classes in S is
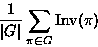
-
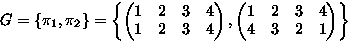
- |G|=2
-
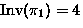
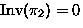
- Burnside's lemma:
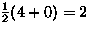 equivalence classes
equivalence classes
- The 2 equivalence classes are
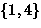 and
and 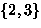
-
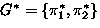
-
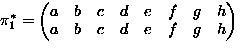
-
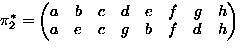
- |G|=|G*|=2
-
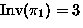 ,
, 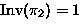 : Burnside
: Burnside 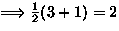
-
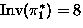 ,
, 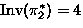 : Burnside
: Burnside 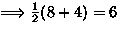
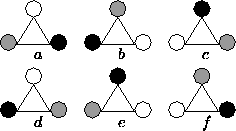
- The 6 equivalence classes are:
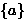 ,
,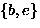 ,
,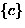 ,
,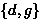 ,
,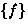 ,
,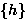
- Note: 4 classes of 1 element, 2 classes of 2 elements
-
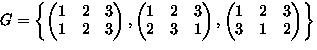
- |G|=3
-
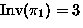 ,
, 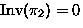 ,
, 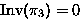
- Burnside lemma:
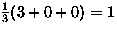 equivalence class
equivalence class
- The single equivalence class is
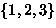
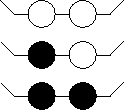
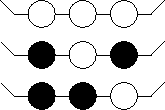
- Three different colored beads
(Black, White, Gray) on an equilateral triangle. Allow rotations.
If

Then the number of distinct colorings in S(D,C) is
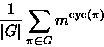
Number of equivalence classes for various k and m
| |
k=2 beads |
k=3 beads |
k=4 beads |
k=5 beads |
k=6 beads |
| m=2 colors |
3 |
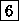 |
10 |
20 |
36 |
| m=3 colors |
6 |
18 |
45 |
185 |
378 |
| m=4 colors |
10 |
40 |
136 |
544 |
2080 |
Let color c have ``weight'' w(c). The pattern inventory describes
the colorings, of a certain kind, as functions of the weights.
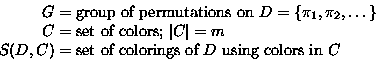
Then the pattern inventory of colorings in S(D,C) is
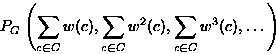
Note: for w(c)=1 have 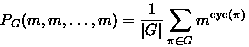
If m=2 colors (Black, White) available:
x1=(B+W),
x2=(B2+W2)
If m=2 colors (B, W) are available, then
If m=3 colors (Black, White, Shade) available:
x1=(B+W+S),
x2=(B2+W2+S2)
- For k=2 have 6 distinct colorings:
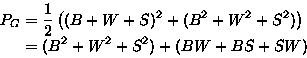
- For k=3 have 18 distinct colorings:
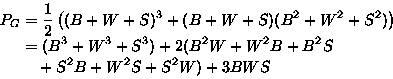
- Many applications of Polya theory:
- bracelets (rotations of an n-gon)
For n=6 find
![$P_G=\frac{1}{6}\left[ x_1^6+x_2^3+2x_3^2+2x_6 \right]$](polya_img147.gif)
- photomasks for chips
- molecular structures
- non-isomorphic graphs
- seating arrangements
- Polya theory is more advanced than shown here
- Daniel Zwillinger can help in formulating and solving discrete
and continuous mathematical problems
(Sudbury 1-1-623, telephone 4-1660)
- 1
-
For pictures of colored necklaces, bracelets, unlabeled necklaces,
etc, visit http://www.theory.csc.uvic.ca/~cos/gen/neck.html
(be careful of terms!)
- 2
-
Harvard Computation Laboratory Staff,
Synthesis of electronic computing and control circuits,
Harvard University Press, Cambridge, MA, 1951.
- 3
-
Fred S. Roberts,
Applied Combinatorics,
Prentice-Hall, 1984.
- 4
-
Sloane's on-line encyclopedia:
http://www.research.att.com/~njas/sequences/
- 5
-
F. Harary and E. Palmer,
``Number of non-isomorphic binary n-state automata'',
Graphical Enumeration, 1973.
- 6
-
Daniel Zwillinger,
CRC Standard Mathematical Tables and Formulae,
CRC,
Boca Raton, FL,
1995.
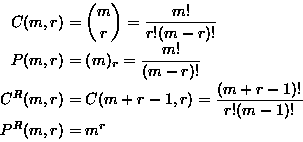
![]()
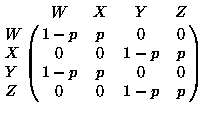
![]()
![]() with
with
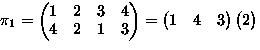
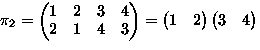
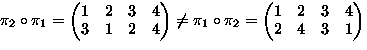
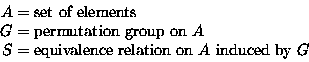
![]()
![]()
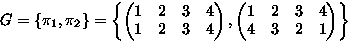
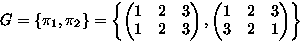
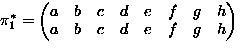
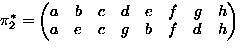
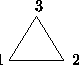
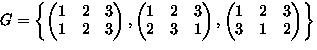
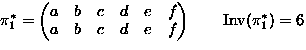
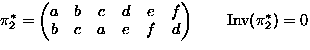
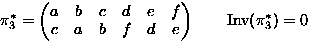
![]() ,
,![]() ,
,![]() ]
]
![]()
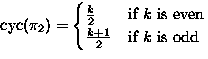
![\begin{displaymath}
\begin{cases}
\frac{1}{2}\left[ m^k + m^{k/2} \right] & \tex...
...m^{(k+1)/2} \right] & \text{if $k$\space is odd} \\
\end{cases}\end{displaymath}](polya_img105.gif)
![]()
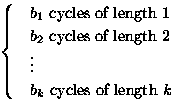
![]()
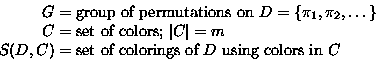
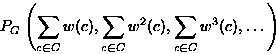
![]()
![]() ,
,![]() and
and
![]()
![\begin{displaymath}
P_G(x_1,x_2)=
\begin{cases}
\frac{1}{2}\left[ x_1^k + x_2^{k...
...2^{(k-1)/2} \right] & \text{if $k$\space is odd} \\ \end{cases}\end{displaymath}](polya_img130.gif)